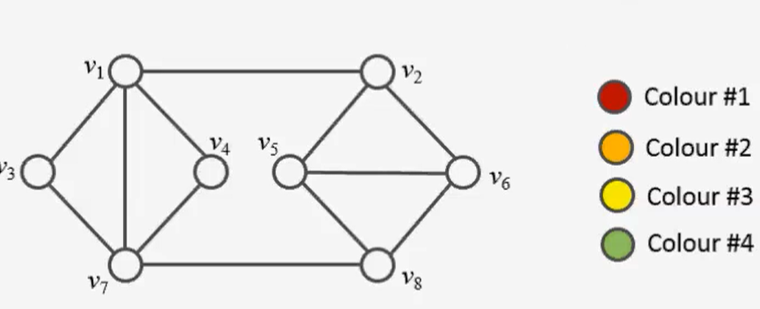
In today’s blog post, let’s dive into the fascinating realm of solving Sudoku puzzles using Mixed Integer Linear Programming (MILP). Check this previous post to see how a sudoku solver can be developed in python using dynamic programming and backtracking. Sudoku, a classic logic-based number placement puzzle, has long captivated minds around the globe with… Read more How to Develop a Sudoku Solver Using Mixed Integer Linear Programming