
In this post I’ll demonstrate the results of my most recent fun project on the micro:bit: An app to solve Happy Cubes®, a set of puzzles created in 1986 by the Belgian toy inventor Dirk Laureyssens. My kids were playing with these cubes and I was wondering, if the micro:bit could solve these cubes in reasonable time. As in my former sudoku solver post, I will use recursive programming with backtracking to tackle this puzzle. Here a few locations, where you can buy Happy Cubes®:
Modeling the Parts
After examining the pieces of the cube, I noticed that all of them consist of a 5 x 5 pattern containing a 3 x 3 filled square in the center.

Therefore each peace can be coded by a series of bits (zeroes and ones), representing the border pattern from every piece’s edge.
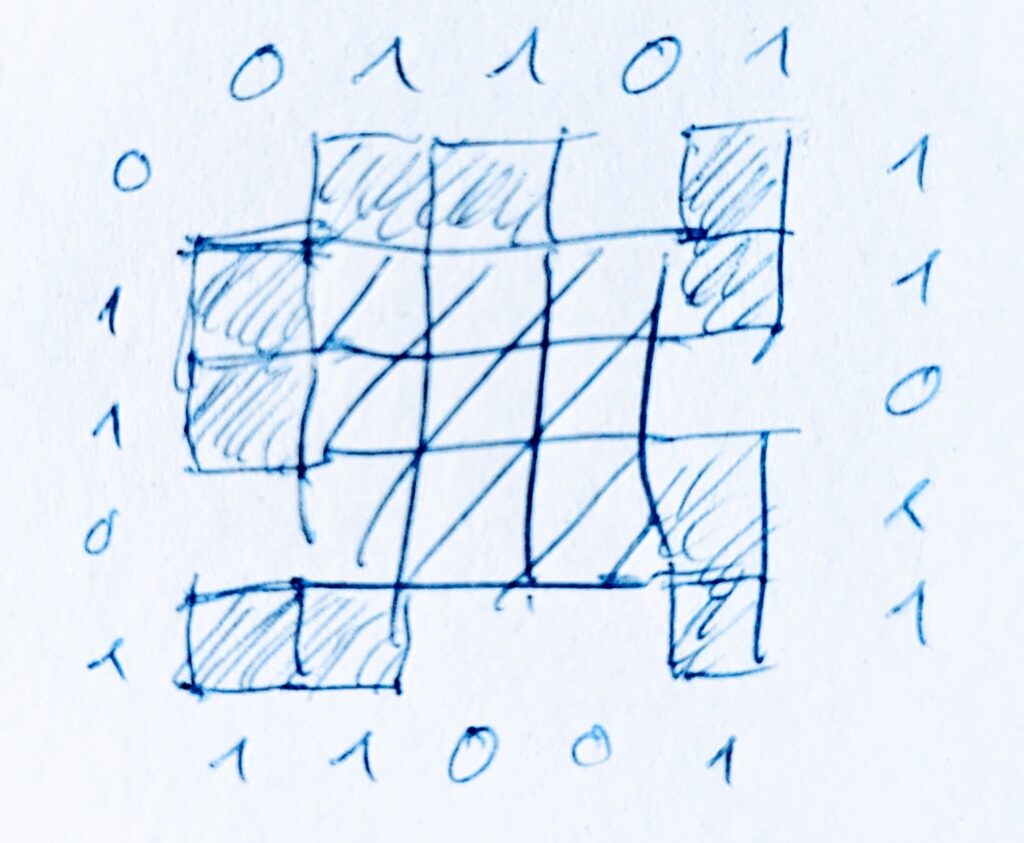
For practical reasons I decided to model the pieces patterns by four 5-bit sequences, one for each edge. In fact, one could cope with 4 bits for each edge, since the corner bits always occur in two adjacent edges. However, the 5-bit version makes comparisons of different edges easier, so I went for this approach.
Modeling the Cube
The cube will be modeled in the form of an ordered sequence of all 6 available pieces and arranged in a cube net, as the following image shows:
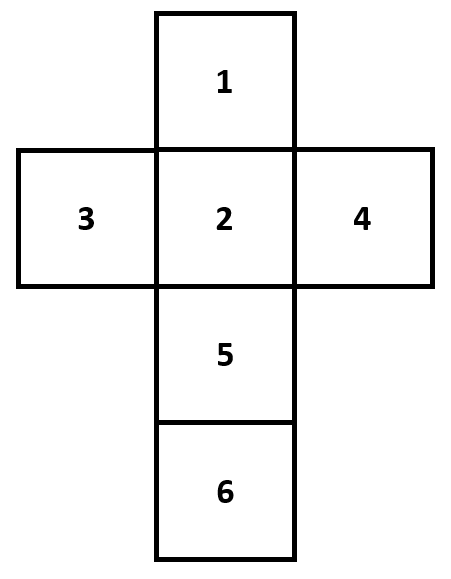
The job of the solver will now be to arrange the available pieces in such a way, that the cube net can be fold together to form a 3D cube. We pretend that the cube will be folded upwards. Face 2 represents the base face and face 6 represents the top face.
How the algorithm works
The algorithm starts with an arbitrarily chosen piece — e.g. the first one provided — in position 1 of the cube net shown above. After that it will try to place the remaining pieces step by step in positions 2, 3 etc. up to position 6. Each piece can be placed in 4 different orientations by rotating it in steps of 90 degrees. In addition, all pieces can also be turned around so that the back side is facing upwards.
This way, the algorithm could generate all possible combinations of parts and will finally find a solution, if one exists. The following function shows the main structure of the recursive solving function:
def solve_cube(cur_sol: Solution):
# get candidate tiles for future moves
cand_tiles = list(set(range(6)).difference(set(cur_sol.tile_sequence)))
cand_tiles.sort()
turnovers = list(range(2))
orientations = list(range(4))
solved = False
for cand_tile in cand_tiles:
for orientation in orientations:
for turnover in turnovers:
if cur_sol.add_tile(cand_tile, orientation, turnover):
if cur_sol.is_solved():
solved = True
break
else:
solve_cube(cur_sol)
if cur_sol.is_solved():
solved = True
break
cur_sol.drop_tile()
if solved:
break
if solved:
break
return cur_solIn each call to solve_cube(), an additional piece for a specific position (1 through 6 in the cube net above) will be placed. If the method fails for all possible combinations in this step, it should return and the caller – i.e. another solve_cube() call – would have to try the next orientation or turnover of the tile considered or even another piece. If the method succeeds, it the current solution is enriched with a next matching piece in a certain orientation and turnover. Then solve_cube() is called recursively to find another matching piece to form the complete cube net.
The piece matching logic is covered in the cur_sol.add_tile() method, which is part of the solution object:
def add_tile(self, tile_id, orientation_id, turnover_id):
if tile_id in self.tile_sequence:
raise ValueError("cannot add tile which is already contained in solution!")
self.tile_sequence.append(tile_id)
self.tile_orient.append(orientation_id)
self.tile_turnover.append(turnover_id)
if self.check_last_tile_valid():
retval = True
else:
retval = False
self.drop_tile()
return retvalThe method adds the new piece (tile) to the solution only, if it matches. It invokes method check_last_tile_valid() in order to verify, whether the most recently added piece in the cube net complies with the gemetric implications. I.e. if a piece is added in position 3 of the cube net shown above, the right edge of piece 3 must match the left edge of piece 2. Additionally, the top edge of piece 3 must match the left edge of piece 1.
How to Define the Cube’s Pieces
Since the pieces consist of a 5×5 matrix, I just used the Image class from the microbit library to represent each of the 6 cube pieces. A specific input method allows the user to set the patterns of the cube pieces using the Buttons A, B to nagivate a blinking cursor within the display border and the touch logo to set / unset pixels:
Button ‘B’ moves the cursor to the right, button ‘A’ to the left and by touching the logo, a pixel is set.

Using the App
After the micro:bit has been flashed with the solver source and the device is connecte to a power source, the app is launched. After the splashscreen text, the app enters the cursor mode and waits for user input to define piece 1 (the app calls the pieces ’tiles’).

The piece’s patterns need to be defined one after the other, starting from left to right and from top to down. It does not matter, how you position and layout the pieces, but you need to remember each piece’s location and index. The solution will be presented in the form ‘Pos 3: R3/L2’. Here, the position number is the position in the cube net shown in the top of this post, starting with 1 at the top of the cube net (position 2 is just beneath position 1, position 3 connects to position 2 on its left hand side, position 4 on the right hand side of position 2 etc.). R3 indicates, that you need to take the third piece in your layout of the pieces show in the picture above and flip it over vertically, so that its back is facing up and its left and right edges swap. Then, finally, L2 indicates, that you need to turn it 2x counterclockwise by 90 degrees.
The following short movie demonstrates, how the solution has to be interpreted in order to assemble the cube.
Complete Source Code
The following listing shows the complete sourcecode of the cube solver. The same source can be obtained here from my github account. It is open source under GPLv3 license.
import utime as time
from microbit import *
class Solution:
cube = {}
tile_sequence = []
tile_orient = []
tile_turnover = []
def __init__(self, cube):
'''
Constructor
:param cube: cube, the solution is tied to
'''
self.cube = cube
# function to check, whether two edges fit into each other
# pos_edge_1, pos_edge_2 are two 2-tuples with tile-id and
# edge-id of the tiles/edges to be compared
def check_edge_compatibility(self, pos_edge_1, pos_edge_2):
tile_id_1 = self.tile_sequence[pos_edge_1[0]]
tile_id_2 = self.tile_sequence[pos_edge_2[0]]
orient_part_1 = self.tile_orient[pos_edge_1[0]]
orient_part_2 = self.tile_orient[pos_edge_2[0]]
turnover_part_1 = self.tile_turnover[pos_edge_1[0]]
turnover_part_2 = self.tile_turnover[pos_edge_2[0]]
edge_id_1 = pos_edge_1[1]
edge_id_2 = pos_edge_2[1]
edge_1_pattern = self.get_cube_line(tile_id=tile_id_1, edge_id=edge_id_1,
orientation_id=orient_part_1, turnover_id=turnover_part_1)
edge_2_pattern = self.get_cube_line(tile_id=tile_id_2, edge_id=edge_id_2,
orientation_id=orient_part_2, turnover_id=turnover_part_2)
retval = True
for i in range(5):
if i == 0 or i == 4:
if edge_1_pattern[i] + edge_2_pattern[4 - i] > 1:
retval = False
break
elif edge_1_pattern[i] != 1 - edge_2_pattern[4 - i]:
retval = False
break
return retval
# function to check, whether a given tile can be inserted as the
# next tile in the given orientation and matches all existing
# tiles pos_ids
# 0
# 2 1 3
# 4
# 5
def check_last_tile_valid(self):
solution_pos_id = len(self.tile_sequence)
retval = False
if solution_pos_id <= 1:
retval = True
elif solution_pos_id == 2:
# only check edges between pos 0 and 1
retval = self.check_edge_compatibility(pos_edge_1=(0, 2), pos_edge_2=(1, 0))
elif solution_pos_id == 3:
# check edges between pos 2 and 1
retval = self.check_edge_compatibility(pos_edge_1=(2, 1), pos_edge_2=(1, 3))
# check edges between pos 2 and 0
retval = retval and self.check_edge_compatibility(pos_edge_1=(2, 0), pos_edge_2=(0, 3))
elif solution_pos_id == 4:
# check edges between pos 1 and 3
retval = self.check_edge_compatibility(pos_edge_1=(1, 1), pos_edge_2=(3, 3))
# check edges between pos 0 and 3
retval = retval and self.check_edge_compatibility(pos_edge_1=(0, 1), pos_edge_2=(3, 0))
elif solution_pos_id == 5:
# check edges between pos 1 and 4
retval = self.check_edge_compatibility(pos_edge_1=(1, 2), pos_edge_2=(4, 0))
# check edges between pos 2 and 4
retval = retval and self.check_edge_compatibility(pos_edge_1=(2, 2), pos_edge_2=(4, 3))
# check edges between pos 3 and 4
retval = retval and self.check_edge_compatibility(pos_edge_1=(4, 1), pos_edge_2=(3, 2))
elif solution_pos_id == 6:
# check edges between pos 4 and 5
retval = self.check_edge_compatibility(pos_edge_1=(4, 2), pos_edge_2=(5, 0))
# check edges between pos 5 and 0
retval = retval and self.check_edge_compatibility(pos_edge_1=(5, 2), pos_edge_2=(0, 0))
# check edges between pos 5 and 2
retval = retval and self.check_edge_compatibility(pos_edge_1=(5, 3), pos_edge_2=(2, 3))
# check edges between pos 5 and 3
retval = retval and self.check_edge_compatibility(pos_edge_1=(5, 1), pos_edge_2=(3, 1))
return retval
# method to remove the last tile from the solution
def drop_tile(self):
solution_pos_id = len(self.tile_sequence)
if solution_pos_id > 0:
self.tile_sequence.pop()
self.tile_orient.pop()
self.tile_turnover.pop()
# method to add a new tile to the solution
def add_tile(self, tile_id, orientation_id, turnover_id):
if tile_id in self.tile_sequence:
raise ValueError("cannot add tile which is already contained in solution!")
self.tile_sequence.append(tile_id)
self.tile_orient.append(orientation_id)
self.tile_turnover.append(turnover_id)
if self.check_last_tile_valid():
retval = True
else:
retval = False
self.drop_tile()
return retval
def is_solved(self):
return len(self.tile_sequence) == 6
def get_cube_line(self, tile_id, orientation_id, turnover_id, edge_id):
'''
return a cube line for a given cube tile, orientation, turnover and edge
:param cube:
:param tile_id:
:param orientation_id:
:param turnover_id:
:param edge_id:
:return:
'''
if not turnover_id:
return self.cube[tile_id][(orientation_id + edge_id) % 4]
else:
line_mapping = {0: 0, 1: 3, 2: 2, 3: 1}
line = self.cube[tile_id][line_mapping[(edge_id + orientation_id) % 4]]
line = line[::-1]
return line
# solve the cube. default the position to be chosen will
# be position id = 1, where a deliberate tile can be chosen
# to start from
def solve_cube(cur_sol: Solution):
# get candidate tiles for future moves
cand_tiles = list(set(range(6)).difference(set(cur_sol.tile_sequence)))
cand_tiles.sort()
turnovers = list(range(2))
orientations = list(range(4))
solved = False
for cand_tile in cand_tiles:
for orientation in orientations:
for turnover in turnovers:
if cur_sol.add_tile(cand_tile, orientation, turnover):
if cur_sol.is_solved():
solved = True
break
else:
solve_cube(cur_sol)
if cur_sol.is_solved():
solved = True
break
cur_sol.drop_tile()
if solved:
break
if solved:
break
return cur_sol
def calc_coord(abs_coord):
dim = 5
x = y = 0
if abs_coord < 5:
x = abs_coord; y = 0
elif abs_coord < 9:
x = 4; y = abs_coord - 4
elif abs_coord < 13:
x = 12 - abs_coord; y = 4
else:
x = 0; y = 16 - abs_coord
return (x, y)
# get an image line from the image representing
# a cube edge in the form of a list containing
# zeroes and ones.
def get_image_line(image, line_id):
line = []
if line_id == 0:
for x in range(5):
if image.get_pixel(x, 0) > 0:
line.append(1)
else:
line.append(0)
elif line_id == 1:
for y in range(5):
if image.get_pixel(4, y) > 0:
line.append(1)
else:
line.append(0)
elif line_id == 2:
for x in range(4,-1,-1):
if image.get_pixel(x, 4) > 0:
line.append(1)
else:
line.append(0)
elif line_id == 3:
for y in range(4,-1,-1):
if image.get_pixel(0, y) > 0:
line.append(1)
else:
line.append(0)
return line
def build_cube(images):
cube = {}
cnt = 0
for image in images:
cube[cnt] = [get_image_line(image, 0), get_image_line(image, 1),
get_image_line(image, 2), get_image_line(image, 3)]
cnt = cnt + 1
return cube
# generate the output string to describe
# the solution cur_sol found
# 'F' means front orientation of the tiles,
# 'R' means flipped orientation of the tiles
# on the vertical axis (so that left / right
# sides of the tiles swap positions)
# pos number indicate the following layout
# of the cube's net:
# 1
# 3 2 4
# 5
# 6
def get_solution_string(cur_sol, i):
front_back_char = "F" if not cur_sol.tile_turnover[i] else "R"
output = "Pos {}: {}{}/L{}".format((i+ 1), front_back_char, cur_sol.tile_sequence[i] + 1, cur_sol.tile_orient[i])
return output
#*******************************************************************************
# main program
#*******************************************************************************
display_scroll_delay = 60
max_coord = 15
tile_id = -1
new_tile = True
cursor_timestamp = time.ticks_ms()
cursor_dt = 500
cursor_state = False
block_touch = False
both_blocked = False
# microbit images for tile-definitions
images = []
display.scroll("* Cube Solver *", delay=display_scroll_delay)
while True:
# preprare new tile
if new_tile and tile_id < 5:
new_tile = False
tile_id = tile_id + 1
display.scroll("Input Tile {}".format(tile_id + 1), delay=display_scroll_delay)
# storage for patterns
images.append(Image())
display.show(Image('00000:'
'09990:'
'09990:'
'09990:'
'00000:'))
abs_coord = 0
x, y = calc_coord(abs_coord)
elif new_tile:
# solve loop: Now start solving
display.scroll("Solving...", delay=display_scroll_delay)
cube = build_cube(images)
cur_sol = Solution(cube)
solve_cube(cur_sol)
break
else:
# handle events
if button_a.is_pressed() and button_b.is_pressed():
if not both_blocked:
new_tile = True
both_blocked = True
else:
both_blocked = False
if button_a.was_pressed():
# paint old position according image data, then move cursor
display.set_pixel(x, y, images[-1].get_pixel(x, y))
abs_coord = abs_coord - 1 if abs_coord > 0 else max_coord
x, y = calc_coord(abs_coord)
elif button_b.was_pressed():
# paint old position according image data, then move cursor
display.set_pixel(x, y, images[-1].get_pixel(x, y))
abs_coord = abs_coord + 1 if abs_coord < max_coord else 0
x, y = calc_coord(abs_coord)
# update cursor
if time.ticks_diff(time.ticks_ms(), cursor_timestamp) >= cursor_dt:
cursor_state = not cursor_state
display.set_pixel(x, y, min(9, 9 * cursor_state + int(images[-1].get_pixel(x, y) * 0.75)))
cursor_timestamp = time.ticks_ms()
if pin_logo.is_touched():
if not block_touch:
if images[-1].get_pixel(x, y) == 0:
images[-1].set_pixel(x, y, 9)
else:
images[-1].set_pixel(x, y, 0)
block_touch = True
else:
block_touch = False
if len(cur_sol.tile_sequence) < 1:
display.scroll("No solution found. ", delay=display_scroll_delay, loop=True)
else:
display.scroll("Cube solved!")
output = ""
i = 0
display.scroll(get_solution_string(cur_sol, i), delay=display_scroll_delay, loop=True, wait=False)
while True:
if button_a.was_pressed():
i = max(0, i - 1)
display.scroll(get_solution_string(cur_sol, i), delay=display_scroll_delay, loop=True, wait=False)
if button_b.was_pressed():
i = min(5, i + 1)
display.scroll(get_solution_string(cur_sol, i), delay=display_scroll_delay, loop=True, wait=False)