TSP Miller-Tucker-Zemlin Subtour Elimination Constraint

Posted on 19. September 202125. September 2021 by Fabian Leuthold

In this post we want to try to provide a solution to solve the Traveling Salesman Problem (TSP) using linear programming. The post is based on this excellent video from Mr. Michel Bierlaire at the EPFL. A good written documentation of the Miller Tucker Zemlin Constraint can be found here.

What is a TSP?

The Traveling Salesman Problem goes as follows:

Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city exactly once and returns to the origin city?
Source: Wikipedia

This problem is one of the most intensely treated tasks in Operations Research.

Historical TSP Contest from Procter & Gabmle in 1962

It is an NP-hard problem and the possible solutions explode exponentially in the number of cities. Even though the problem is computationally difficult, many heuristics and exact algorithms are known, so that instances with tens of thousands of cities can be solved.

TSP solved using Linear Programming

Now let’s try to solve the TSP using a linear model. Consider the following graph with the cities 1-5:

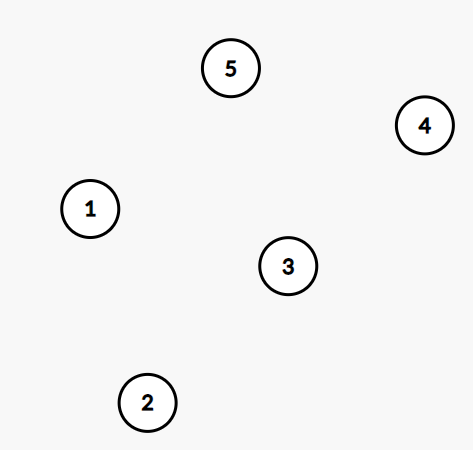
Five cities to visit using the shortest tour

In order to minimize the TSP tour we need to know the distance between all nodes. Let $d_{ij}$ denote the distance between the nodes $i$ and $j$ . Now in order to model this as an optimization problem, we need:

decision variables
objective function
constraints

Let $x_{ij}$ be our binary decision variables, telling us, whether node $j$ is visited directly after node $i$ ( $x_{ij}=1, \; 0$ otherwise).

Since we know the distance between all nodes ( $d_{ij}$ ), together with $x_{ij}$ we can now write down our objective function which minimizes the total distance of our TSP tour:

$min \; z = \sum_{(i,j)} x_{ij} \cdot c_{ij}$

Now let’s think about the constraints we need to establish, in order to get valid TSP tours. After a bit of reflection, one might come up with the followin two ideas:

Constraint 1: Every node has exactly one successor node.

$\forall i \sum_j x_{ij} = 1$

Constraint 2: Every node has exactly one predecessor node.

$\forall j \sum_i x_{ij} = 1$

If we would try to solve the problem above with the 5 cities using the model above, we might get a solution as follows:

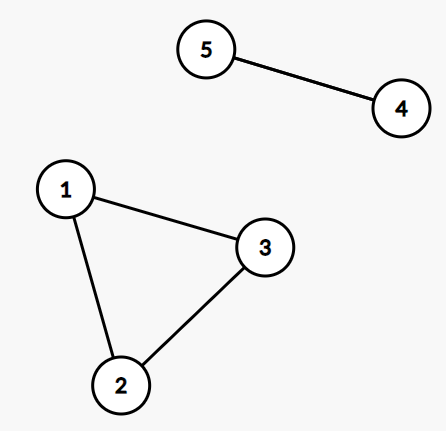
As can be seen, not all nodes are connected to one single tour. The resulting tour consists of two unconnected subtours: Tour 1-2-3-1 and tour 4-5-4. Although this tour is not a valid TSP tour we can easily determine that both constraints are met. Our model obviously does not prevent our solution to consist of unconnected subtours. We need a so called subtour elimination constraint to prevent the situation above.

There are multiple ways to prevent subtours. Here, we have a look at one possible approach known as the Miller-Tucker-Zemlin Subtour Elimination Constraint (MTZ-STE).

A first Subtour Elimination Constraint (STE)

The core idea here is to suppress subtours is to enumerate all but the start location in the resulting tour. If we can make sure, that the first stop after the depot gets assigned index 1 and every subsequent stop in the tour gets a succeeding integer index assigned compared to its predecessor, we could eliminate unconnected subtours. The MTZ formulation goes as follows:

$u_1 = 1$
$\forall i \ne 1: \;\; 2\le u_i \le n$
$\forall i \ne 1, \forall j \ne 1: \;\; u_i - u_j +1 \le (n-1)(1-x_{ij})$

Let’s check, whether this makes sense. If $x_{ij} = 1$ , we get:

$u_i - u_j +1 \le 0 \implies u_j \ge u_i + 1$

This is exactly what we want. Every subsequent node gets assigned an index which is at least 1 larger than the index of its predecessor. If $x_{ij} = 0$ , we get:

$u_i - u_j +1 \le n-1$

Also this is true, since the largest difference between two indexes of any (non start) nodes equals to $n - 2 + 1 = n - 1$ , which is exactly what’s written here.