There are situations where you might want to use a specific Mathematical Programming solver and you might have to transform the mathematical model to comply with the API specifications of that Solver. Here I want to show you, how to adapt a Linear Model in order to run it within Matlab using the Gurobi solver.
A simple Integer Linear Program
To show, what transformations have to be applied in order to migrate a linear model from matlab to Gurobi using the matlab-gurobi API, let’s start with a simple linear model. Let’s say, we have to solve the following integer linear model:
![]()
s.t. ![]()
![]()
![]()
![]()
In matrix notation we’d have:
![]()
s.t ![]()
Since we have only 2 decision-variables here, we can easily solve the model graphically:
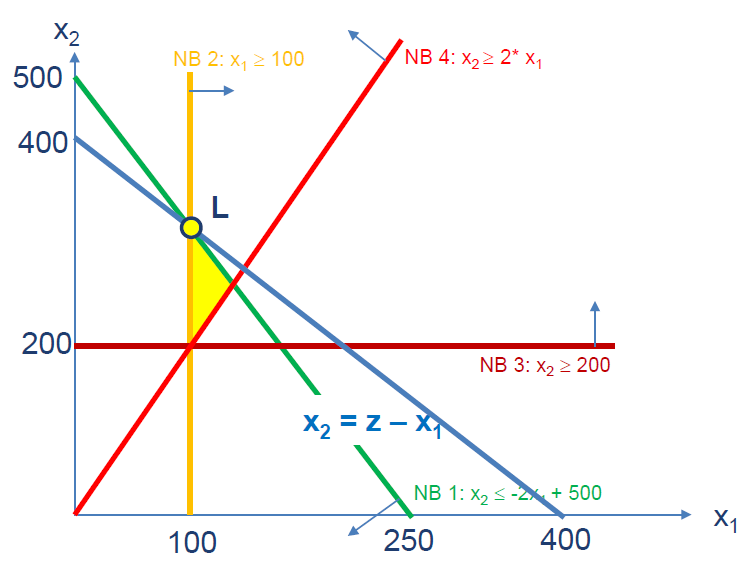
We can see, that the objective function reaches it’s maximum for ![]() and
and ![]() .
.
Solve the Model with Matlab
In order to solve this integer linear program in Matlab we would have to apply the following modifications:
- Multiply the objective function by (-1), since we want to do maximization, whereas matlab always does minimization (and therefore also multiply the objective value of the result by (-1))
- Convert all constraints showing
 signs to constraints showing
signs to constraints showing  signs.
signs. - Provide the constraints being equations in the specific arguments provided (you don’t have to convert equations to combinations of
 and
and  )
)
% objective function vector without constant-term
f = [-1, -1]';
% indexes of integer decision variables
intcon = [1, 2]';
% A-Matrix
A = [800, 400;-1, 0; 0, -1; 2, -1];
% RHS vector
b = [200000, -100, -200, 0]';
% solver call (
x = intlinprog(f,intcon,A,b)
[colX,numFval,numExitflag,sOutput] = intlinprog(f,intcon,A,b)There are different versions of the intlinprog – command providing additional arguments, details see here. The matlab output after running the script above would look something like this:
Optimal solution found.
Intlinprog stopped at the root node because the objective value is within a gap tolerance of the optimal value,
options.AbsoluteGapTolerance = 0 (the default value). The intcon variables are integer within tolerance,
options.IntegerTolerance = 1e-05 (the default value).
colX =
100
300
numFval =
-400As we can see, we have to multiply numFval by (-1) to get the correct output-value of the objective function, since we negated the objective-function to be able to transfer the problem into a minimization problem.
Solve the Model with GUROBI
In order to have the GUROBI commands available in Matlab, you first need to have a working GUROBI Solver installation, a valid license and have run the matlab_setup.m Matlab – Script, coming with GUROBI Solver. See this post, to find a detailled overview on the steps necessary to install GUROBI Solver as well as how to obtain a commercial or academic license.
In order to solve the same model with gurobi, we have to prepare a struct and pass the arguments as described in the reference manual. When consluting the documentation of the matlab API, you realize, that there is no possibility to provide ![]() or
or ![]() constraints in the model, only ‘<‘, ‘>’ and ‘=’ are allowed. (in the documentation it is even stated to accept only ‘=’ – constraints).
constraints in the model, only ‘<‘, ‘>’ and ‘=’ are allowed. (in the documentation it is even stated to accept only ‘=’ – constraints).
However, it turns out that ‘<‘ and ‘>’ are takten as ‘![]() ‘ and ‘
‘ and ‘![]() ‘, when solving ILPs. First I introduced slack variables to be able to model ‘
‘, when solving ILPs. First I introduced slack variables to be able to model ‘![]() ‘ and ‘
‘ and ‘![]() ‘ constraints but then I realized, that this is not necessary. One can just provide the model as follows:
‘ constraints but then I realized, that this is not necessary. One can just provide the model as follows:
% objective function
model.obj = [1,1]';
% signs-vector
model.sense = ['<', '>', '>', '<']';
% right hand side
model.rhs = [200000, 100, 200, 0]';
% lower bounds for decision vars
model.lb = [0,0]';
% upper bounds for decision vars
model.ub = [1e22, 1e22]';
% var types: Integer
model.vtype = ['I', 'I']'
% our matrix
model.A = sparse([800, 400; 1, 0; 0, 1; 2, -1]);
% optimization directive
model.modelsense = 'max';
params.outputflag = 0;
result = gurobi(model, params);
result.xWhen running this script, gurobi would deliver the following expected solution:
ans =
100
300
ans =
400